
一起来看看博弈论是个什么方法,什么理论,解决什么问题。

1 | 目录 · · · · · · |
第一章 博弈三要素与囚徒困境
博弈三要素
参与者、策略以及博弈所得(支付,盈利)
囚徒困境
两个理性参与者在面对选择时的决策困境。具体情境如下:
假设有两个犯罪嫌疑人,甲和乙,他们因一起犯罪被警方逮捕,但警方缺乏足够的证据来定罪。于是,警方将他们隔离审讯,并提供给他们一个选择:
坦白:如果一个人选择坦白并指控另一个人,而另一个人保持沉默,坦白的人将被释放,而沉默的人将入狱五年。
沉默:如果两人都选择沉默,由于证据不足,他们将各自入狱一年。
互相指控:如果两人都选择坦白,他们将各自入狱三年。
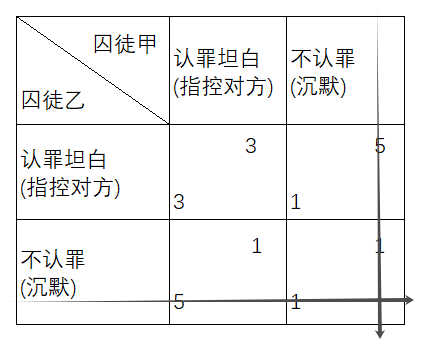
尽管合作(即两人都选择沉默)能带来较轻的惩罚(各入狱一年),但由于缺乏信任和对对方行为的不可预知性,理性的参与者往往会选择坦白,以期望获得更好的个人结果。这导致了一个悖论:如果两人都追求个人利益,最终的结果却是两人都比合作的结果更糟(各入狱三年)。因此,囚徒困境揭示了个体理性选择与集体最优结果之间的矛盾。
严格优势策略均衡
指的是在一个博弈中,参与者选择的策略都是严格优势策略,并且在这种情况下,任何参与者都没有动力单方面改变自己的策略,因为改变策略会导致其收益下降。
具体来说,严格优势策略是指对于某个参与者而言,不论其他参与者选择什么策略,选择该策略的收益总是大于选择其他任何策略的收益。
而严格优势策略均衡则是指在这个均衡状态下,所有参与者都选择了自己的严格优势策略,结果形成了一种稳定的局面,任何参与者都不会通过单方面改变策略来提高自己的收益。
囚徒困境是一种严格优势策略均衡
其他的囚徒困境模型
- 公共品供给的囚徒困境
两个邻居张三和李四,他们都可以选择是否修一条路出去。修路的好处是每家都能得到好处,但修路的成本则需要共同承担。如果两家都不修路,大家都得零;如果一家修而另一家不修,修路的一家会亏损,而不修的一家则可以坐享其成。
因此,在缺乏协调的情况下,双方都可能选择不修路,导致最终的结果是无人修路,大家都得不到好处。
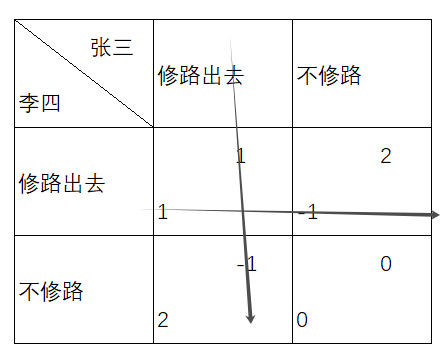
这种情形体现了囚徒困境的核心:个体在追求自身利益的同时,忽视了集体利益,最终导致集体的损失。解决公共品供给的囚徒困境,往往需要政府或其他机构的介入,以协调各方的利益,确保公共品的供给。
- 政治家的囚徒困境
描述政治家在面临公共政策决策时所面临的博弈情况。在这个博弈中,政治家们知道如果他们能够合作,共同采取某种政策(例如增加税收或削减开支),将对国家整体利益有利,但由于各自担心对方不合作而导致自己承担更大的政治风险,他们往往选择保持被动,不主动提出合作方案。
在这个博弈中,参与者是民主党和共和党。假设两党都意识到,面对巨额预算赤字,采取合作措施(如增税)将是对国家最有利的选择。然而,任何一方如果主动提出增税,可能会遭到选民的反对,损害自己的政治前途。于是,双方都选择保持沉默,导致最终的结果是没有采取任何行动,赤字问题依然存在。
这个博弈的支付矩阵可以表示为:如果两党都主动合作,各自的利益会相对较好;如果一方合作而另一方不合作,合作的一方将承担政治代价,而不合作的一方则可能获得更多的选民支持;如果两党都不合作,结果则是对国家和两党的长远利益都是不利的。
总结来说,政治家的囚徒困境展示了在缺乏信任和合作的情况下,理性政治家可能会选择不合作的策略,尽管合作对整体利益是最有利的。这种现象反映了在政治决策中,个人利益与集体利益之间的矛盾。
- 美苏争霸的囚徒困境
在冷战时期,美国和苏联这两个超级大国在军事和核武器扩张上的相互博弈。在这个博弈中,双方都有两种策略可供选择:一种是扩军发展核武器,另一种是裁军。根据博弈的设定,如果双方都选择扩军,各自的成本都很高,最终的结果是双方都损失;如果双方都选择裁军,则可以避免不必要的开支,达到零成本的状态。
然而,由于在一个弱肉强食的国际环境中,任何一方如果选择裁军而另一方选择扩军,裁军的一方将面临巨大的风险,可能会被对方欺凌和损害。因此,从各自的利益出发,双方都倾向于选择扩军。这样一来,尽管扩军对双方都是不利的选择,但由于缺乏信任和合作的可能性,最终导致了双方都陷入了扩军的困境。
这个博弈的核心在于,虽然合作裁军是对双方都有利的选择,但由于缺乏信任和对对方行为的担忧,最终导致了双方都选择了对自己不利的扩军策略,形成了一个典型的囚徒困境。通过这一例子,可以深刻理解博弈论中理性主体在面对相互依赖的情况下,如何因自利行为而导致非最优的集体结果。
第二章 情侣博弈和协调博弈
情侣博弈
在情侣关系中,双方由于偏好不同而面临的选择困境。这个模型通常涉及到两个人在周末或假期选择活动时的决策,比如一方想看足球,而另一方则希望去看芭蕾舞。尽管双方的偏好不同,但他们最不愿意的事情是各自单独去做自己喜欢的事情,而是希望能够一起度过这段时间。
在情侣博弈中,双方的满意程度取决于他们的选择。例如,如果两人一起看足球,大海(喜欢足球)会非常高兴,而丽娟(喜欢芭蕾)虽然不太满意,但仍然比各自去看自己喜欢的节目要好。相反,如果两人都去看芭蕾,丽娟会非常开心,而大海则会感到不满意。若两人各自去做自己喜欢的事情,则双方的满意程度都为零。
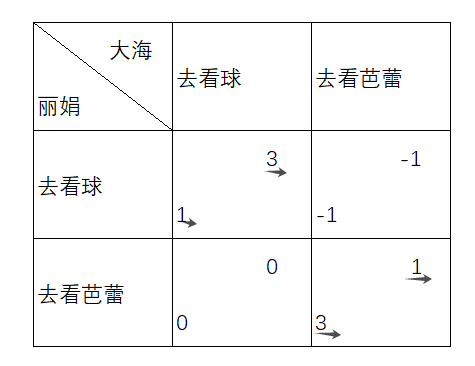
这一博弈的核心在于纳什均衡的概念,即在某种策略组合下,任何一方都没有单独改变策略的激励,因为这样做不会带来更好的结果。在情侣博弈中,可能存在多个纳什均衡,例如双方一起看足球或一起看芭蕾,这两种选择都是稳定的结果,因为一旦达成这样的选择,双方都不想单独改变策略。
通过情侣博弈,博弈论可以揭示出在面对不同偏好时,如何通过协调和妥协来实现双方的满意度最大化。这一模型不仅适用于情侣关系,也可以扩展到其他类型的合作关系中,例如朋友、同事或商业伙伴之间的决策。
纳什均衡
纳什均衡是指在一个博弈中,所有参与者在给定其他参与者策略的情况下,选择自己最优策略的状态。在这个均衡状态下,没有任何一个参与者能够通过单方面改变自己的策略而获得更好的结果。
通过情侣博弈的例子,讲述了纳什均衡的具体表现。比如,大海和丽娟这对情侣在选择周末活动时,可能面临一起看足球或一起看芭蕾的选择。在这种情况下,如果两人都选择了看足球或都选择了看芭蕾,那么他们的满意程度都达到了相对的最优,形成了纳什均衡。在这两个均衡中,任何一方单独改变选择都不会带来更好的结果,反而可能导致满意度下降。
总结来说,纳什均衡强调的是在一个多方参与的决策环境中,如何在相互依赖的情况下达到一种稳定的策略组合,确保每个参与者的选择都是基于对其他参与者选择的合理预期。
囚徒困境也是一种纳什均衡。
情侣博弈的其他例子
电影选择博弈:假设一对情侣想去看电影,男方喜欢动作片,而女方喜欢爱情片。如果两人都选择自己喜欢的电影,他们可能会各自去看,导致双方的满意度都为零。如果他们选择一起去看某一部电影,比如一部兼具动作和爱情元素的影片,他们的满意度会提高。
度假目的地博弈:情侣计划度假,男方想去海滩,女方想去山脉。如果他们各自选择自己喜欢的地方,可能会导致不满。最佳的选择是一起去一个两人都能接受的目的地,比如一个有海滩和山脉的地方。
晚餐选择博弈:情侣在决定晚餐时,男方想吃快餐,而女方想吃健康餐。如果他们各自坚持自己的选择,可能会导致分开就餐。通过妥协,比如选择一家既提供快餐又有健康选项的餐厅,他们可以达到双方都满意的结果。
购物决策博弈:在购物时,男方可能更倾向于购买电子产品,而女方可能想买衣服。如果他们分开行动,可能会导致各自不满意的选择。通过一起讨论,他们可以找到一个购物中心,既有电子产品也有时尚服装,从而满足双方的需求。
这些例子展示了情侣之间在面对不同偏好时如何通过协调与妥协来实现共同的满意度,这正是情侣博弈的核心思想。通过理解和应用博弈论的纳什均衡概念,情侣可以在选择中找到最佳的合作策略。
情侣博弈表达的对称性嗜好
模型中将两个人独自选择不喜欢的活动(如大海独自看芭蕾,丽娟独自看足球)设定为零的满意度,反映了这种对称性:两人各自选择不喜欢的活动会导致双方都不满意,因此更倾向于选择共同的活动,尽管这个活动可能不是各自的最爱。这种对称性使得博弈的结果更具稳定性和可预测性,反映了人际关系中的合作与协调。
总之,情侣博弈中的对称性嗜好强调了参与者在选择策略时的平衡与一致性,尽管各自的偏好不同,但他们都希望在关系中找到共同的满足点。
理性不等于自私自利
在现代经济学中,理性人的假设并不等同于自私自利。理性人是指那些在既定约束条件下,努力实现自身目标最大化的个体。理性行为的核心在于明确的目标函数,而这个目标函数可以是多种多样的。
例如,一个人的目标函数可能是个人财富的最大化,这种情况下,他的行为可能看似自私自利。然而,另一些人的目标函数可能是他人幸福和快乐的最大化,比如父母为孩子的幸福而努力,这样的行为就体现了对他人的关心和付出。
因此,理性人并不必然是自私自利的。相反,许多行为看似不自利,但在理性人的框架下,仍然可以被理解为合理的选择。例如,母亲宁愿自己吃剩饭,也要让孩子享受美食,这种行为反映了她对孩子幸福的追求,而不是单纯的自我利益。
总之,理性人的行为是多元的,关键在于其目标函数的设定,而非简单地将其归结为自私自利。
自利行为并非一无是处
在现代经济学中,自利行为并不一定是负面的。自利行为是指个体在追求自身利益最大化的过程中,所采取的行动。实际上,理性经济主体的行为是为了在既有的约束条件下,努力实现自己的目标函数的最大化。这样的行为不仅符合个人的利益,也能在一定程度上促进社会的整体发展。
首先,许多经济活动的推动力源于个体的自利行为。例如,企业为了追求利润最大化,往往会提升产品质量、降低价格,从而使消费者受益。这样的市场竞争机制不仅能促进经济发展,还能提高资源的配置效率。
其次,自利行为并不意味着对他人的损害。许多时候,个体在追求自身利益的同时,也在为他人创造价值。例如,母亲为孩子的幸福而努力工作,这种行为看似是出于自利,但实际上也体现了对他人的关爱和责任。
最后,经济学中的“看不见的手”理论表明,个体在追求自身利益的过程中,往往会无意中促进社会的整体福利。因此,完全贬斥自利行为是不合理的。我们应当认识到,自利行为在适当的条件下,能够与他人的利益相结合,形成双赢的局面。
总之,自利行为并非简单的自私,而是一种复杂的社会现象。在理解和评价自利行为时,我们应考虑其对个人和社会的双重影响,而不是一味地贬斥。
协调博弈
情侣的拥挤博弈
情侣的拥挤博弈是一种博弈论中的模型,主要用于描述情侣在特定环境下的决策过程,尤其是在资源有限的情况下如何选择。视频中提到的情境是,假设在一个小公园里只有两张椅子可供情侣休息,而在周末时,有两对情侣希望去公园。这种情况下,每对情侣的选择会影响到彼此的满意程度。
在这个博弈中,情侣们面临以下选择:
两对情侣都去公园,导致拥挤,满意程度较低。
一对情侣去公园,另一对情侣留在家中,满意程度较高。
通过博弈矩阵的分析,可以发现这个博弈有两个纳什均衡:
一对情侣去公园,另一对情侣留在家中。
另一对情侣去公园,第一对情侣留在家中。
在这两种情况下,情侣们的满意程度都相对较高,且任何一方都没有单独改变策略的激励,因为这样做不会带来更好的结果。
这种拥挤博弈的分析揭示了在有限资源下,情侣之间如何协调以实现更好的结果,同时也反映了在社会生活中人们如何通过默契和合作来优化决策。
默契是协调的一种方式
默契被称为协调的一种方式,是因为在多个参与者的博弈中,默契可以帮助他们在没有明确沟通的情况下,自然地达成一致,从而选择一个对所有参与者都有利的策略组合。在博弈论中,特别是在协调博弈中,参与者的目标往往是选择相同的策略,以实现共同的利益。
例如,在视频中提到的情侣拥挤博弈中,参与者需要在去公园和待在家之间做出选择。如果两对情侣都能形成默契,约定这次由一对情侣去公园而另一对情侣留在家中,下一次再反过来,那么他们就能够避免拥挤,达到各自满意程度的最大化。这种默契的形成,实际上是一种非正式的协调方式,能够使参与者在没有外部干预的情况下,找到一个稳定的均衡点。
因此,默契不仅是一种社交行为,也是一种有效的策略选择机制,使得参与者能够在复杂的决策环境中,依靠彼此的理解和信任,顺利达成共识,优化各自的收益。
第三章 简单博弈模型的应用
博弈过程中的风险厌恶
智猪博弈和搭便车
有两只猪——一只大猪和一只小猪,它们被放在一个长笼子里。笼子的一端有一个按钮,按下按钮可以获得相当于十个单位的猪食,但按按钮和跑到食槽所需的劳动消耗相当于两个单位的猪食。问题在于,按钮和食槽分别位于笼子的两端。
如果两只猪同时按下按钮并跑向食槽,大猪能吃到七个单位的食物,小猪能吃到三个单位的食物。
如果大猪按下按钮而小猪先跑到食槽,大猪能吃到六个单位的食物,而小猪能吃到四个单位。
如果小猪按下按钮而大猪在食槽旁边,小猪能吃到一个单位的食物,而大猪能吃到九个单位的食物。
如果两只猪都不动,什么也得不到。
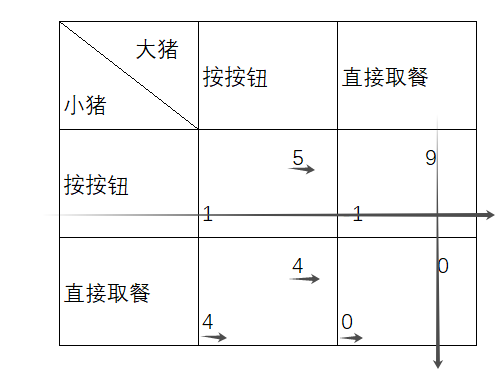
通过这些选择,智猪博弈展示了参与者在面对利益冲突时的策略选择。大猪由于其体型和优势,通常能够占据食槽,而小猪则往往选择等待,以便享受大猪按按钮后带来的食物。最终,博弈的均衡结果是小猪通过搭便车的方式,坐享其成。
智猪博弈不仅适用于描述动物行为,还可以用于解释经济学中的搭便车现象和公共品提供的问题,展示了在缺乏协调和合作的情况下,个体如何在博弈中追求自身利益,可能导致的非最优结果。
为什么大股东挑起监督经理的重任
大股东挑起监督经理的重任主要是因为他们在公司中的利益与小股东相比,具有更高的利益攸关程度。在视频中提到,假设公司运营良好,大股东的分红可能增加一千万元,而小股东的分红仅增加一万元。在这种情况下,大股东会更愿意投入时间和资源去监督经理的工作,因为即使花费几万元或十几万元来监督,也能换来近千万元的分红增加,这样的投资回报率是非常高的。
相对而言,小股东因为监督成本与潜在收益之间的差距,往往缺乏足够的激励去密切监督经理的工作。他们可能会选择“搭便车”,依赖大股东的监督成果而自己不付出相应的努力。因此,在这种博弈中,大股东承担了监督经理的责任,而小股东则相对被动地享受大股东的努力带来的收益。这种现象在经济学中被称为“智猪博弈”,强调了在资源配置和利益分配中的不平等和不同角色的行为差异。
猎人博弈
猎人博弈是一种博弈模型,通常用于描述两个猎人之间的合作与竞争关系。在这个模型中,猎物的获取依赖于猎人的合作,但猎人也可能选择各自独立行动,从而影响各自的收益。
在猎人博弈中,假设有两个猎人,主要猎物有两种:鹿和兔子。为了捕获鹿,两个猎人必须合作;而如果单独行动,他们只能捕获兔子。具体来说,假设猎人A和猎人B的收益如下:
- 如果两人合作猎鹿,他们可以捕获一只鹿,并平分猎物,每人获得10天的食物。
- 如果两人都选择单独猎兔子,他们各自能捕获4只兔子,每人获得4天的食物。
- 如果一人选择猎鹿而另一人选择猎兔,选择猎鹿的猎人将一无所获,而选择猎兔的猎人可以获得4只兔子。
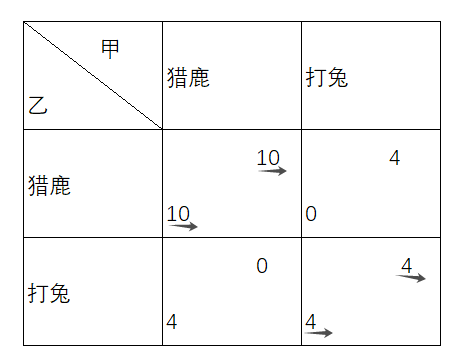
在这个博弈中,有两个可能的纳什均衡:
- 两个猎人都选择合作猎鹿,获得较高的收益。
- 两个猎人各自选择猎兔,虽然收益较低,但在没有合作的情况下这是他们的最佳选择。
猎人博弈的核心在于分析合作的利益与个人利益之间的权衡,以及在缺乏信任或协调机制的情况下,参与者可能会选择的行为模式。这一模型可以帮助理解在现实生活中,个体如何在合作与竞争之间做出选择,以及如何通过制度设计来促进合作。
帕累托优势
帕累托优势是经济学中一个重要的概念,用于描述资源配置的效率。在一个经济体中,当一种资源的配置状态达到帕累托优势时,意味着在不损害其他任何人的情况下,无法再改善某个人的境况。换句话说,如果想要改善某一个人的福利,就必须以另一个人的福利为代价。
在博弈论的背景下,帕累托优势通常与纳什均衡相对立。一个博弈的纳什均衡并不一定是帕累托最优的,可能存在其他状态可以使某些参与者的得益增加而不损害其他参与者的得益。
例如,在猎人博弈中,如果两个猎人选择合作一起猎鹿,他们的总收益会高于各自单独猎兔的情况。在这种情况下,合作猎鹿的结果就具有帕累托优势,因为两位猎人都能获得更大的收益,而不需要损害对方的利益。
帕累托优势的概念强调了资源的有效利用和分配的重要性,特别是在公共品的提供和合作博弈中,能够有效地引导参与者寻求共同的利益和最大化整体的福利。
斗鸡博弈和航行规则
斗鸡博弈是一种经典的博弈论模型,其名称源于儿童游戏中,两个孩子在独木桥上相向而行,谁先退让谁就被视为“胆小鬼”。在这个博弈中,两个参与者面临两个选择:勇敢地向前走或者退让。博弈的结果取决于双方的选择,可能出现的结果包括:一方勇敢而另一方退让,勇敢者获胜;双方都退让,皆可保全面子;或者双方都勇敢,导致两败俱伤。
具体来说,斗鸡博弈的支付矩阵可以表示如下:
如果一方勇敢而另一方退让,勇敢者得4分,退让者得2分。
如果双方都退让,各得3分。
如果双方都勇敢,则都得0分。
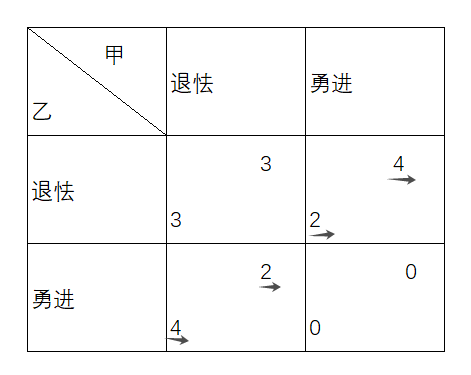
这个博弈的纳什均衡有两个:其中一方勇敢而另一方退让。
航行规则则是基于斗鸡博弈的思想,应用于海上航行中船舶交汇的情况。为了避免碰撞,许多国家制定了航行规则,例如:当两艘船相向而行时,双方应各向右偏移一点,以便安全通过。这种制度设置可以看作是对斗鸡博弈的一种规范化,通过明确的规则引导船舶行为,从而减少碰撞的风险。
在航行规则的博弈中,双方的选择仍然会影响最终的结果,若双方都选择不让行,可能会导致碰撞;若双方都选择让行,则能安全通过。因此,航行规则的制定不仅是为了确保安全,也是为了通过制度引导参与者做出理性的选择,实现双赢的局面。
银行挤兑的成因和预防
在银行挤兑博弈模型中,储户的选择可以分为两种策略:等待到期取款或提前取款。模型的支付矩阵显示,如果双方都选择等待到期取款,他们各自能获得更高的收益(例如每人获得120万元)。然而,如果一方提前取款,而另一方选择等待,提前取款的储户将获得100万元,而等待的储户则可能只能获得40万元,这种情况下,提前取款的储户获得了较大的利益。
然而,若两位储户都选择提前取款,银行将无法满足他们的需求,导致每人只能获得70万元。因此,这个博弈有两个纳什均衡:一个是双方都选择等待取款,另一个是双方都选择提前取款。
预防:
- 提高透明度:通过定期公布银行的财务状况和投资情况,增强储户的信心。
- 建立准备金制度:确保银行有足够的流动资金来应对储户的提前取款需求。
- 政府担保:政府可以对存款提供保险,增加储户的安全感,从而降低挤兑的可能性。
囚徒困境两败俱伤的隐含条件
双方势均力敌,如果一方远远强大于另一方,则情况就不一样了。
案例:禁鸣喇叭与交通顺畅
通过修改支付金额,造成双方的”势均力敌”或者”差距悬殊”避免囚徒困境,形成纳什均衡。可以有效解决现实中的囚徒困境问题。
风险优势
风险优势是博弈论中的一个概念,主要指在不确定的环境中,参与者选择某种策略时能够降低潜在风险的优势。在博弈中,参与者通常会考虑各种可能的结果及其对应的概率,以此来做出理性的决策。
具体来说,风险优势体现在参与者在面对不确定性时,选择一个相对稳妥的策略,以避免可能的极端损失。例如,在某个博弈中,如果一个参与者选择了一个风险较小的策略,虽然这个策略的收益可能不如高风险策略的潜在收益高,但由于其风险较小,参与者在多次博弈中能够获得更稳定的回报。
相关的博弈案例:
- “最惠客待遇”对谁有利
- 禁鸣喇叭与交通顺畅
- 营造克己奉公的制度环境
总的来说,风险优势强调在决策过程中,选择能够降低风险的策略,尽管这些策略的收益可能不是最高的,但在不确定的环境中能够提供更大的安全感和稳定性。
风险优势和帕累托优势
帕累托标准和风险标准之间,理论给帕累托优势以优先权,而风险优势只有在局中人面临不知道选哪个均衡的不确定性的时候才变得重要。
风险厌恶就是边际效用递减规律
是一致的,家里几个亿的有钱人,损失10块钱的风险厌恶 小于 月薪2000元的人损失10块钱。 反着说就是边际效用递减:损失10块钱随着收入的增多边际效用递减。
第四章 混合策略与均衡筛选
零和博弈
案例:扑克牌对色游戏
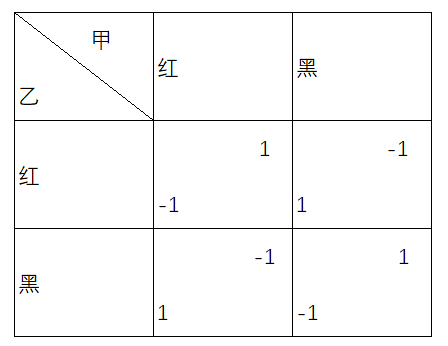
每一局对局博弈的结果都是要么你输一根火柴,我赢一根火柴。 但是总支付的和 1+(-1)总是等于0, 这就是零和博弈。
混合策略和纳什定理
扑克牌对色游戏中,有出红牌和黑牌两种纯策略。
还有以p的概率出红,以1-p的概率出黑牌的 混合策略。
纳什定理:如果允许混合策略,那么每个有限同事博弈都有纳什均衡。
证明相当困难。
寻找纳什均衡的反应函数法
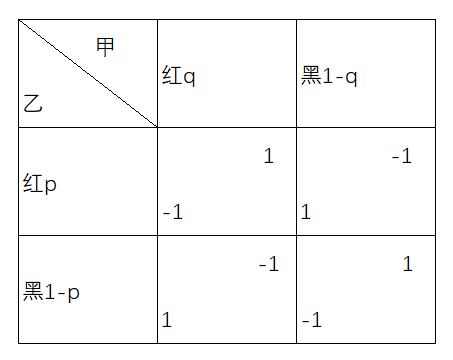
对甲来说: 求期望:
U甲(p,q)= pq1 + (1-p)*q * (-1) + (1-q)p * (-1) + (1-p)(1-q)*1
= pq - q + pq - p + pq +1 -p - q +pq
= 4pq -2p -2q +1
= 2p(2p-1) - (2p-1)
= (2p-1)(2p-1)
所以,参与人乙对于参与人甲的策略,选择的反应函数:
q = 1 如果 p > 1/2
q=[0,1] 如果 p = 1/2
q = 0 如果 p< 1/2

反之同理,综合求得
p = 1/2
q = 1/2就是纳什均衡
再说混合策略纳什均衡
改变支付,纳什均衡求解就会改变,会产生更多的规律~~~~~
案例:
- 扑克牌讹诈游戏
- 慕尼黑谈判模拟
聚点均衡
据点均衡是博弈论中的一个概念,主要由学者谢林提出。它指的是在多重纳什均衡的情况下,参与者通过一些共同的、显而易见的信号或约定,来选择一个特定的均衡作为博弈的结果。这种均衡往往与参与者的社会文化习惯、过去的博弈经历等因素密切相关。
在实际生活中,参与者可能会利用某些被广泛接受的约定或信号来达成共识,从而选择一个相对稳定的均衡。例如,在情侣博弈中,双方可能会选择一起看球或一起看芭蕾,具体的选择可能受到双方的默契、约定或特定情境的影响。
据点均衡的关键在于,它能够帮助参与者在众多可能的均衡中,聚焦于一个更有可能实现的结果。这种选择通常是基于共同的理解或社会文化背景,而不仅仅是理性计算的结果。
总结来说,据点均衡强调的是参与者在面对多重均衡时,如何通过共同信号或约定,选择一个更稳定、更具可预见性的均衡结果。
- 聚点均衡作为共识均衡
- 聚点均衡的制度设置
相关均衡
相关均衡是博弈论中的一个重要概念,由奥曼在1974年提出。它的基本思想是参与者通过一个大家都能够观察到的共同信号来选择行动和策略,从而确定博弈的最终结果。
在相关均衡中,参与者不仅考虑自己的策略选择,还会考虑其他参与者的选择,以及这些选择如何受到共同信号的影响。这种信号可以是事先商定的,也可以是博弈过程中自然产生的信息。例如,参与者可能会根据某种外部条件(如天气、市场情况等)来调整自己的策略。
相关均衡的关键在于,参与者的策略选择是相互关联的,即他们的决策不仅基于自身的利益,还受到其他参与者的行为和共同信号的影响。这种均衡状态通常比传统的纳什均衡更具稳定性,因为它能更好地反映参与者之间的相互依赖关系。
总结来说,相关均衡强调了信息共享和策略关联的重要性,能够帮助分析在复杂博弈中如何通过共同信号达成更优的决策。
- 商品品牌的“地域连坐”效应
- 品牌地域连坐的博弈分析
抗共谋均衡
抗共谋均衡是博弈论中的一个概念,旨在解决多参与者博弈中可能出现的共谋行为。它的基本思想是,在一个博弈的均衡状态下,不仅要求参与者在该状态下没有单独偏离的激励,还要求他们在集体层面上也没有共谋偏离的激励。
具体来说,抗共谋均衡的特点包括:
单独偏离无好处:在抗共谋均衡中,任何参与者如果单独改变自己的策略,都不会获得更好的结果。
集体偏离无激励:在抗共谋均衡中,参与者之间的集体偏离策略也没有激励。也就是说,即使多个参与者联合起来改变策略,他们的收益也不会增加。
稳定性:抗共谋均衡比一般的纳什均衡更具稳定性,因为它排除了参与者之间的共谋行为,这种行为可能导致博弈结果的不确定性和不稳定性。
通过引入抗共谋均衡的概念,博弈论能够更好地分析和预测在复杂的多参与者环境中,参与者如何选择策略,以及如何避免因共谋而导致的非理性行为。这一概念在经济学、政治学以及其他社会科学领域的研究中具有重要的应用价值。
- 盯着不散伙的共谋
- 德国世界杯警方的优势策略
第五章 零和博弈与霍特林模型
零和博弈与非零和博弈
零和博弈是指在博弈中,参与者的利益总和始终为零。换句话说,一个参与者的收益恰好等于另一个参与者的损失。在这种博弈中,任何一方的得益必然是另一方的损失。例如,扑克牌对策游戏就是一个典型的零和博弈。在这个游戏中,如果你赢得了一根火柴,那么对手就相应地失去了一根火柴。由此可见,零和博弈强调的是参与者之间的对抗性,任何一方的成功都意味着另一方的失败。
非零和博弈则是指参与者之间的利益关系并不局限于零和的状态。在这种博弈中,参与者可以通过合作实现双赢或多赢的局面,即所有参与者的得益之和可以大于零。非零和博弈的一个经典例子是囚徒困境。在这个博弈中,如果双方都选择合作,他们都能获得较低的刑期,实现双赢;而如果双方都选择背叛,则最终都将面临更长的刑期,导致双输的局面。
零和博弈强调的是对抗性和竞争性,而非零和博弈则更注重合作和共赢的可能性。这两种博弈模型帮助我们理解不同情况下的决策行为和策略选择。
均衡的观察与验证
大胆假设,小心验证
许多重大的科学发现,都是科学家凭借直觉或者归纳分析出的可能命题,然后严密的科学论证。
纳什均衡的精髓是,没有一个人有动机单独的偏离当前的策略选择。
比如假设两个人分100块钱,每个人独立给出自己想要的金额,然后写在纸上给主持人,主持人根据两个人的金额之和是否大于100来判断,如果大于100,双方都一分钱拿不到,如果小于100,都能拿到自己想要的。
直觉高速我们,50,50 应该是一个纳什均衡。
确实,局中人在不改变对方50的前提下,想最大化收益,写51则一分钱拿不到,写40则还不如50,所以这就是一个纳什均衡。
打开格局,任何(a,b) a+b = 100都是一个纳什均衡,对不对!!!
霍特里模型与纳什均衡
霍特林模型是博弈论中的一个重要模型,主要用于分析在特定市场环境下的竞争行为,尤其是如何选择最优的地理位置以吸引顾客。该模型由经济学家霍特林提出,通常用于描述两个或多个参与者在一条直线上的位置选择问题。
在霍特林模型中,假设有两个商家(例如杂货铺)在一条均匀分布的道路上开店,顾客会选择离自己最近的商家购买商品。为了最大化各自的市场份额,两个商家都希望选择一个最优的位置。霍特林模型的关键在于,尽管商家可能希望在道路的两端开店以覆盖更多顾客,但实际的博弈结果往往是两家商家会选择挤在一起,通常是在道路的中间位置。
具体来说,霍特林模型的纳什均衡状态是,当两家商家都选择在相同的位置时,任何一方单独改变位置都不会获得更大的市场份额。这种现象表明,在竞争中,商家之间的相互作用会导致一种稳定的竞争状态,尽管这种状态可能并不是最优的社会福利配置。
霍特林模型不仅适用于商业竞争分析,还可以扩展到政治竞争、社会选择等领域,帮助理解不同参与者如何在资源有限的环境中做出策略选择。
霍特林模型案例:杂货铺定位
杂货铺定位问题是博弈论中的一个经典模型,最早由经济学家霍特林提出。这个问题主要探讨在一个居民区内,两个或多个杂货铺如何选择开店位置,以最大化自己的市场份额。
在这个模型中,假设居民住宅沿着一条公路均匀分布,两个杂货铺(A和B)销售相同的商品,价格也相同。顾客会选择离自己最近的杂货铺进行购物。由于每个杂货铺都希望吸引尽可能多的顾客,他们的目标是尽量靠近对方,以争夺中间顾客的市场份额。
在理想情况下,两个杂货铺的最佳位置应该分别在公路的四分之一和四分之三的位置,这样可以使每个杂货铺的市场份额各占一半。然而,由于每个杂货铺都希望占据更多的市场份额,它们会相互挤压,最终导致两个杂货铺都选择在公路的中间位置开店。这种情况下,虽然它们都在争取顾客,但最终却都无法实现最优的市场分配,反而增加了顾客的行走距离。
这一现象展示了博弈论中的纳什均衡,即在某种策略组合下,任何一方单独改变策略都不会获得更好的结果。在杂货铺定位问题中,当两个杂货铺都选择在中间时,任何一方都没有动力去改变自己的位置,因为这样会导致顾客的流失。
所以只要承认理性人假设,两家挤在中点就是唯一稳定的策略选择,是唯一的纳什均衡。
霍特林模型案例:西方两党政治的稳定性和欺骗性
西方两党政治的稳定性和欺骗性主要体现在两个方面:政治竞争的动态和选民行为的变化。
首先,从政治竞争的动态来看,西方的两党制通常由两个主要政党主导,如美国的民主党和共和党,英国的保守党和工党。这些政党在选举期间会争取更多的选民支持,因此它们的政策纲领往往会趋向于彼此靠近,以吸引中间选民。这个过程可以用霍特林模型来解释:两个政党为了争夺选票,都会调整自己的政策立场,最终导致两者在政策上几乎没有实质性差异,形成一种竞争中的“挤压”效应。这种现象使得两党在选民眼中看似提供了选择,但实际上政策的差异性却大大降低,从而导致政治的欺骗性。
其次,从选民行为的角度来看,选民在投票时往往会受到信息的不对称和政治宣传的影响。在选举期间,政党会通过各种手段来吸引选民,往往会夸大自己的政策效果或贬低对手的缺点。这种情况下,选民可能会在选举时做出基于情感或短期利益的选择,而不是基于长远的政策分析。这种现象加剧了政治的欺骗性,因为选民可能会在选举后发现,新的执政党并没有实现其竞选时所承诺的政策。
因此,西方两党政治的稳定性源于两党之间的竞争和选民的投票行为,而其欺骗性则体现在政策的相似性和选民对政党的期望与实际结果之间的差距。这种现象不仅影响了政治的透明度,也使得选民对政治的信任度降低。
摊贩都往市场门口挤
也是霍特里模型的一种。
学校门口等出租车的争先行为
也是霍特里模型的一种。
多人博弈的霍特林模型
当2人博弈时, 纳什均衡是(1/2,1/2)
当3人博弈时,没有纳什均衡
当4人博弈时,纳什均衡是(1/4,1/4,3/4,3/4)
当5人博弈时,纳什均衡是(1/6,1/6,3/6,5/6,5/6)
…
对抗性排序
你死我活的扑克牌对色游戏博弈
出现双赢可能的价格战囚徒困境博弈
个体利益与集体利益基本一致的情侣博弈
以上有强到弱
协调博弈
协调博弈是一种博弈类型,其中参与者的利益在某种程度上是一致的,合作通常会导致更好的结果。在协调博弈中,参与者之间存在共同的目标,选择相同的策略往往会带来双赢的局面。
协调博弈可以分为广义和狭义两种:
广义协调博弈:包括所有可能协调出双赢对局的博弈,即使是像囚徒困境那样需要附加条件并且多次重复才能实现双赢的博弈,也算在内。
狭义协调博弈:专指个体利益与集体利益基本一致的博弈。在这种博弈中,合作总是比不合作更有利。例如,在情侣博弈中,双方都希望通过合作实现共同的利益。
协调博弈的一个经典例子是交通规则博弈。在没有交通规则的情况下,两个司机如果都靠右行驶,交通就会顺畅,双方各得一分;如果一个司机靠右而另一个司机靠左,则会发生事故,双方都得负分。因此,遵循共同的交通规则可以确保双方都能获得最佳的结果。
在协调博弈中,虽然参与者可能会面临不同的选择,但通过有效的沟通和合作,他们能够找到最优的策略组合,从而实现双赢。
第六章 动态博弈和子博弈精炼均衡
序贯博弈
什么是序贯博弈
序贯博弈是博弈论中的一种博弈形式,主要特点是参与者的决策是按照时间顺序进行的,而不是同时作出决策。在序贯博弈中,某些参与者在其他参与者做出决策后再进行决策,这种决策的先后顺序会影响博弈的结果。
“抓钱博弈”就是一个典型的序贯博弈示例。在这个博弈中,参与者甲和乙轮流做出决策,甲首先决定是否拿走面前的金额,如果他选择不拿,接下来乙会做出决策,依此类推。每一轮的决策不仅依赖于当前的选择,还受到之前决策的影响。
序贯博弈通常用树形图表示,每个节点代表一个决策点,参与者在这些节点上选择策略。树形表示法可以清晰地展示出每个参与者的决策顺序和可能的结果,帮助分析博弈中的纳什均衡和子博弈精炼均衡等概念。
贯博弈强调决策的时间顺序和信息的流动,能够更好地反映现实生活中许多决策过程的复杂性。
抓钱博弈,不通规则制度,结果不通,说明博弈结果依赖制度设置。
实验经济学和行为经济学
许多经济学实验都是从博弈论开始。
- 本文标题:读《平话博弈论》
- 本文作者:形而上
- 创建时间:2024-05-30 12:00:00
- 本文链接:https://deepter.gitee.io/2024_05_30_game_theory/
- 版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!